February 2022
Title: Exploring stability behaviour in magnetism.
Description: Magnetism can be described by ordinary and partial differential equations. Controlling its stability behaviour is often desirable for various physical reasons. This can be difficult to achieve and heavily dependent on the differential equation. Some mathematical tools and concepts related to the analysis of stability of differential equations are: (i) linearization (ii) Lyapunov theory (iii) modelling (iv) norms and Lp spaces (v) vector operations, (vi) simulations in MATLAB, and lastly (vii) a general willingness to talk to others about what you don’t know.
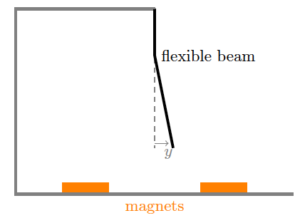
Pictured above is the displacement effects of magnetism on a flexible ferromagnetic beam.
Who are the collaborators? This is a joint project with the University of Waterloo, and hence an ideal networking opportunity to meet other students, educators, professors and researchers outside of York University. Here is more information of the research group,
https://uwaterloo.ca/applied-mathematics/research-links/research-groups/infinite-dimensional-systems-research-group
What is the format? This project will require a mixture of online and in-person activities. Some time spent physically in an experimental math space and physically at the University of Waterloo may be required. In-person activities will depend on university policies.
What are the student’s primary responsibilities? independent reading and learning with good time management, conducting literature searches, applying mathematical knowledge creatively and correctly, attending teaching and research meetings, writing mathematical solutions, programming in MATLAB.
What are some York math courses related to this project? math 2270, math 3271, math 4271 and knowledge of real analysis
What technical skills are required? MATLAB and LaTeX; depicted below are some samples of MATLAB simulations related to this project. The looping behaviour in both diagrams indicates multistability in the dynamics of the differential equation.
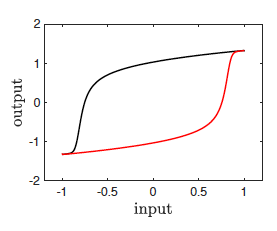
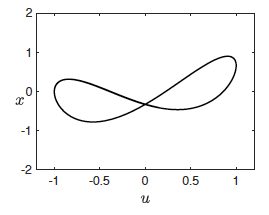
Who would supervise you?
Amenda Chow (York), primary contact, amchow@yorku.ca, https://amchow.info.yorku.ca
Kirsten Morris (Waterloo), https://uwaterloo.ca/applied-mathematics/people-profiles/kirsten-morris
Here are some references related to this project:
- S. Afshar, K. Morris, and A. Khajepour, Hysteresis in pde model of a li-ion battery, in Proceedings of the American Control Conference, Piscataway, NJ, USA, 2016, pp. 4362-7.
- A. Chow and K. Morris, Hysteresis in the linear landau-lifshitz equation, in Proceedings of the American Control Conference, 2014.
- A. Chow and K. A. Morris, Control of the Landau-Lifshitz equation, Automatica, 67 (2016), pp. 200 - 204.
- B. Guo and S. Ding, Landau-Lifshitz Equations, vol. 1 of Frontier Of Research with the Chinese Academy of Sciences, World Scientific, 2008.
- K. Hassan, Nonlinear Systems, Prentice Hall, 3rd ed., 2002.
- L. Landau and E. Lifshitz, On the theory of the dispersion of magnetic permeability in ferromagnetic bodies, Ukrainian Journal of Physics, 53 (2008), pp. 14-22.
- K. Morris, What is hysteresis?, Applied Mechanics Reviews, 64 (2011).
- J. Oh and D. Bernstein, Semilinear duhem model for rate-independent and rate-dependent hysteresis, IEEE Trans. Autom. Control (USA), 50 (2005), pp. 631- 45.
- L. Perko, Differential Equations and Dynamical Systems, Springer, 2002.