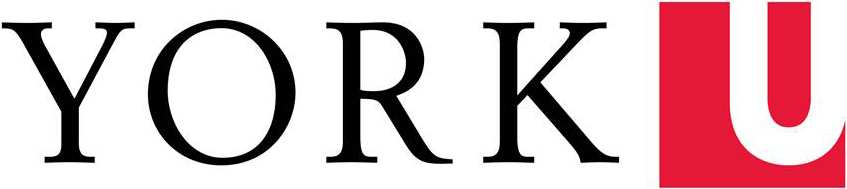Acquired in 2024:
43. The card game UNO.

42. Cross math is similar to scrabble but instead of constructing words, mathematical equations are constructed. Playing cross math re-enforces concepts about arithmetic and numeracy.

41. Apply spatial reasoning and logic to play "Tiltago". Move around this cross shaped object so that the numbers on the marbles are placed in order or arrange into the colours of the rainbow.

Acquired in 2023:
40. A theremin is the only musical instrument that is played without touching it. Notes and volume are controlled by motions of the hand near the instruments antennas. This is an ideal instrument to motivate the mathematics behind vibrations. In the EMS we have a Theremini created by Moog Music, pictured below.

39. Use mathematical logic to play the game of set, which requires "matching" cards into groups of three based on four attributes: colour, number, style and shape, each of which has to all match or all be different. This a fun game to play in groups and in collaboration. An online version can be found here. A related card game called Qwirkle Rummy requires matching based on colour and shape, and is often played in a more competitive setting.
 .
. 
38. This loop-the-loop track demonstrates the interchange between kinetic and potential energy for a marble rolling along the tracks. Also learn more about the appearance of quantities like gravity, height, radius and velocity and the role they play in the physical world.

37. Shown below is a projectile launcher with a range of about 8 metres. It can be used to demonstrate such concepts as distance, trajectories, angles, and speed.

36. Learn about moment of inertia by rotating each wand. Notice the difference? What is causing the difference?

35. Spin a volunteer with their arms outstretched sitting on the(green) rotational turntable stool. As the stool is rotating ask that they tuck their arms inward towards their chest. What happens? What if the volunteer held a one kg mass in each hand? What happens when one of the masses is tossed and caught? Or if the volunteer was holding a spinning object like a bicycle wheel or standing (rather than sitting)? The rotational turntable stool and wheel demonstrates conservation of angular momentum, torque, gyroscopic motion and rotational kinetic energy.


34. The zoetrope is a device used to make simple animations, much like a flip book does. Its cylindrical shape with see through slots is the key to creating the animation when spun and viewed by the human eye. Pictured below is the animation of a person bouncing a ball on their knee. The illusion of motion depends two behaviours involving the human eye: persistence of vision and phi phenomenon. Explore the zoetrope by spinning it in different directions and at varying speeds, viewing the animation from different angles, creating different drawings for the animation or making your own zoetrope using household objects. Similar devices to the zoetrope include the thaumatrope, praxinscope, and mutoscope.

33. The abacus was used for counting in ancient times. It can be considered the predecessor to modern day calculators. Learning to operate the abacus will help with understanding basic arithmetic such as addition/subtraction and multiplication/division. It can also be a tactile learning tool for more advanced topics like modular arithmetic.

32. The Brachistochrone Problem is an often classic problem in calculus of variations. It was posed by mathematician Johann Bernoulli (1667 - 1748) which he stated as follows: given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time? Learn more about the history of this problem here.
To experimentally explore this problem, Professor Chris Bergevin from the Department of Physics and Astronomy, and his student (Juntung Jiang) kindly 3d-printed us a model to test three paths. A video can be found here.

Acquired in 2022:
31. Learn about rotational motion, balancing, spinning and energy by experimenting with a gyroscope. Here is a video of it in motion, and below is a black and white drawing indicating each component of the gyroscope pictured on the left.


30. Create pleasing and intricate spiral patterns using a geometric design device known as a spirograph. The spirograph uses motions of circles and various geometry concepts to produce its designs.


29. Explore light refraction, reflection and kaleidoscopes using this right angle prism.

28. The scifi tube showcases our body's ability to conduct electricity. By touching this tube, complete the circuit necessary to light it up and make sounds. Here's a video demonstrating this. Try it with others by making a circuit with multiple people. What happens?

27. A rattleback is a semi-ellipsoid shaped object that has a preferred direction of rotation regardless of which direction it is initially spun. This is due to its shape. Here's a video showing this.

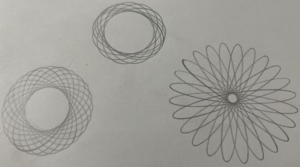
26. Microscopes from Carson Optics will allow exploration of the mathematics that appears in our microscopic world such as the edges and vertices of graphs, fractals, tessellations, etc. The function of microscopes also relates to concepts about numeracy such as measurements, scales and decimals, and hence lends itself as a technological tool and manipulative for mathematics education.
We have two types of Carson Microscopes. The one depicted on the left is a digital microscope that displays magnified images onto the computer screen which allows for further manipulation and analysis. The second shown on the right is more portable and images can be captured on a phone using the smartphone adapter clip. 

Below are some images taken from these microscopes. On the left, the computer screen shows the image of a magnified rock, and the remaining two objects are taken from a smartphone with the middle depicting fibers of a pair of black denim jeans, and the image on the right is human hair.


25. This resonance bowl, when filled with water, generates standing waves along the edge of the water as its handles are rubbed. This bowl first appeared more than two thousand years ago (Han Dynasty), was believed to promote strength, happiness and longevity. The resulting sound is also intriguing and can be measured and analyzed using a mobile app like Phyphox. A video of it can be found here. Learn more about the science and history here.

Acquired in 2020:
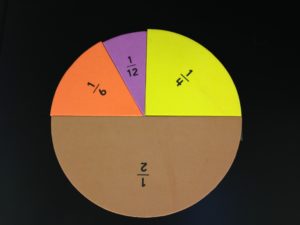
24. These magnetic foam fraction circles are a fun way to learn about arithmetic, especially fractions, and encourage team work for young leaners. These were used in Math 4100 (Topics in Math Education) for our teacher candidates. Credit: Professor Andrew Skelton.
23. Roll this Tumble 'N Teach Dice! Operations are on the outside and two dies are on the inside. These dies are a fun way to integrate arithmetic, randomization and physical activity for young leaners. These were used in Math 4100 (Topics in Math Education) for our teacher candidates. Credit: Professor Andrew Skelton.

22. Cuisenaire rods are tactile aids that explore arithmetic, especially fractions, for young leaners. These were used in Math 4100 (Topics in Math Education) for our teacher candidates. Credit: Professor Andrew Skelton.

21. Attribute math blocks are tactile aids that explore such as concepts as geometric shapes, patterns, arithmetic, Venn Diagrams and mathematical reasoning for young leaners. These were used in Math 4100 (Topics in Math Education) for our teacher candidates. Credit: Professor Andrew Skelton.

Acquired in 2019:
20. This experiment creates standing waves in a string using a string vibrator. Both ends of the string are fixed, and nodes/antinodes are clearly visible. The vibrating string experiment was used at the CMS Math Summer Camp and Math Circles to demonstrate experimental math, mathematical modelling and vibrations. A video can be found here. Credit: Professor Hongmei Zhu.

19. These double length slinkies (152cm in length) aid in the visualization and generation of waves, and hence model vibrations and ideas related to it such as amplitude, frequency, period, oscillation, sinusoidal curves, etc. These slinkies were used at the CMS Math Summer Camp to demonstrate experimental math, mathematical modelling and vibrations. Credit: Professor Hongmei Zhu.

18. Similar to the zoomtools (item 17 below), polydron frameworks are manipulative tools for building and exploring geometric shapes. The cube pictured below is constructed from polydron frameworks. These were used in Math 4100 (Topics in Mathematical Education) and Math 3052 (Exploring Geometries). Credit: Professor Andrew Skelton and Professor Walter Whiteley.

17. Zometools are manipulatives that facilitate the visualization and construction of geometric shapes. These were used in Math 4100 (Topics in Mathematical Education). The blue and yellow cube like structure in the picture below was constructed from zometools. Credit: Professor Andrew Skelton and Professor Walter Whiteley.

16. This is a mirascope (15cm in diameter) which can be used to create a hologram. The mirascope consists of two parabolic shaped mirrors facing each other. The top mirror has a hole in its centre. The actual frog is placed at the bottom of the mirror. Through reflections between the two mirrors, an image of the frog appears on top of the hole. Here is a schematic of how the mirascope works.

15. This is a resonance experiment, which consists of Chladni plates (in the shape of a 24cm sided square, 24 cm diameter circle, 40cm long violin shape), a mechanical wave driver and a sine wave generator. The plate sits on top of the mechanical wave driver which creates vibrations that are controlled by the sine wave generator. Sand is sprinkled evenly on top of the vibrating plate, and eventually the sand settles to stable nodes creating symmetric patterns, called Chladni figures, that can be predicted by the wave equation and elasticity theory. A video of this can be found here. This is a classic experiment first made famous by Ernest Chladni (1756 - 1827).

The appearance of the Chladni figure depends on the shape of the plate and the frequency of the sine wave generator. The mathematical theory behind Chladni figures was derived by Sophie German (1776 - 1831). This experiment was used at the Fields Institute "A Celebration of Women Mathematicians" (May 13, 2019) and during our CMS summer math camps. The experiment can be simplified to the one-dimensional case by replacing the plates with a string. Credit: Allysa Lumley, Yohana Solomon and Professor Hongmei Zhu.



14. A disc and circle of the same size and weight are racing down a ramp. Which one always wins the race? This demonstration was used in Math 2015 (Applied Multivariate and Vector Calculus) to motivate moments of inertia. It was also used in Math 3010 (Vector Integral Calculus). Here is a professor video explaining the relationship between moment of inertia and this experiment. Credit: Professor Andrew Skelton.

13. This is a Sphero Bolt, which is an app-enabled robot with a 7.3cm diameter. It was used in Math 2015 (Applied Multivariate and Vector Calculus), Math 3052 (Exploring Geometries), and MATH 4100 (Topics in Mathematical Education). Examples of mathematical concepts that the Sphero Bolt will help students learn include graphing, geometry, parameterizations and programming. It was also used for a student math project about finding the optimal path on the plane given obstacles along the path, which required programming into the sphero bolt a shortest path algorithm known as Jarvis’ March and explored mathematical concepts such as convex hulls and optimization. Credit: Professor Andrew Skelton.

Acquired in 2018:
12. This is a rotary servo base unit (approximately 15cmX15cmX18cm) from Quanser, which steers the dynamics of mounted or attached appendages such as a pendulum, flexible link or joint, and beam. The software this rotary unit uses is MathWork's Simulink. It was used in Math 3052 (Exploring Geometries) and MATH 4650 (Feedback Control Systems).

11. This is a ball on a beam (length is 42.55cm) with one end of the beam fixed and the other end attached to a rotary servo base unit (approximately 15cmX15cmX18cm) that controls the movement of the ball and beam. This apparatus is from Quanser. To hold the ball at equilibrium on the beam requires stability theory and feedback control. The software this rotary unit uses is MathWork's Simulink. It was used in Math 3052 (Exploring Geometries) and MATH 4650 (Feedback Control Systems).


10. This is a pendulum (length is 33.7cm) which attaches to a rotary servo base unit (approximately 15cmX15cmX18cm) from Quanser. To invert the pendulum requires stability theory and feedback control. See this video of the pendulum inverted and self-correcting (re: applying feedback) to maintain its inverted position. The software this rotary unit uses is MathWork's Simulink. It was used in Math 3052 (Exploring Geometries) and MATH 4650 (Feedback Control Systems).


9. This is a flexible link (length is 41.9cm) mounted on a rotary servo base unit (approximately 15cmX15cmX18cm) from Quanser. It is often used to model vibrations in flexible structures, such as the wing of an airplane, and feedback control. Here is a video of its dynamics. It can also be used to model medical ailments such as tremors in limbs that arise as a symptom of a disease. The software this rotary unit uses is MathWork's Simulink. It was used in Math 3052 (Exploring Geometries) and MATH 4650 (Feedback Control Systems).

8. This is a coupled tanks system (approximately 30.5cm X 30.5cm X 91.5cm) from Quanser. The software this coupled tanks system uses is MathWork's Simulink. It was used in Math 3052 (Exploring Geometries), MATH 3250 (Mathematical Biology), MATH 4090 (Mathematical Modelling) and MATH 4650 (Feedback Control Systems). Credit: Professor Jane Heffernan.

7. This is a Lego Mindstorm EV3 (approximately 15cm X 19cm X 12cm), which is a programmable robot based on Lego building blocks. The corresponding software for these robots is available here. It was used in Math 3052 (Exploring Geometries), MATH 3250 (Mathematical Biology) and MATH 4090 (Mathematical Modelling). Credit: Gian Alix; Emily Di Bratto; Gina Faraj; Professor Jane Heffernan; Spencer Hooks; Professor Andrew Skelton.
See what other's are doing with the EV3:
https://www.ucalgary.ca/IOSTEM/robot-tasks/robot-challenges
http://www.stemcentric.com/ev3-tutorial

6. This is a water tank (approximately 101.5cm x 15cm x 31cm) that generates waves by way of a compressed air generator. Instructions on how to use this can be found here. The study of waves explores mathematical concepts such as amplitude, sinusoidal functions, estimation, frequency, cycloids, etc. Credit: Kaloyan Bankov; Louis Conforti; Kevin Yu.

5. This 3D printed piece (approximately 10cm x 10cm x 10cm) is a hypercube. It was used in Math 3052 (Exploring Geometries). Credit: Professor Andrew Skelton; Thingiverse; Shapeways.

4. This 3D printed "wobbly circle" piece (approximately 6cm x 12cm x 7cm) was obtained for teaching the idea of circles and how they move. It was used in Math 3052 (Exploring Geometries). The inspiration for this piece can be found here. Credit: Professor Andrew Skelton; Thingiverse; Shapeways.

3. This 3D printed piece (approximately 6cm x 7cm x 10cm) is a Klein Bottle. It was used in Math 3052 (Exploring Geometries) in F2018-W2019. Credit: Professor Andrew Skelton; Thingiverse; Shapeways.

2. This 3D printed piece (approximately 8cm x 8cm x 10cm) is a Sierpinksi Pyramid. It was used in Math 3052 (Exploring Geometries). Credit: Professor Andrew Skelton; Thingiverse; Shapeways.

1. This 3D printed piece (approximately 8cm x 10cm x 8cm) was obtained for teaching the idea of stereographic projections. It was used in Math 3052 (Exploring Geometries). Credit: Professor Andrew Skelton; Thingiverse; Shapeways.

This page was last updated on December 21, 2024; it was first created on September 11, 2018.